Collaborators: L. Vitos and A. Ruban (KTH, Stockholm)
The Exact Muffin-Tin Orbitals (EMTO) method is an improved screened Korringa-Kohn-Rostoker (KKR) approach that allows exact calculation of the one-electron Kohn-Sham states, and consequently the one-electron total energy, for optimized overlapping muffin-tin (MT) potentials by using a Green's function formalism. Within the framework of the EMTO method, in contrast to the usual muffin-tin based KKR methods that assume no-overlapping MT potentials, large, overlapping potential spheres can be used for an accurate representation of the exact one-electron potential. The EMTO formalism allows keeping the simplicity and efficiency of traditional MT methods and, at the same time, avoids the negative effects of the shape approximations employed for the potential and density. Therefore, the EMTO theory provides an ideal ground for the development of an accurate and efficient full charge density based method for pure elements, compounds and random alloys. The EMTO Theory was developed by O. K. Andersen (MPI, Stuttgart) [1]. L. Vitos implemented the theory within the spherical cell approximation and combined it with the Full Charge Density technique and the Coherent Potential Approximation (CPA) [2-5]. Today the EMTO-CPA method opens unique possibilities in the field of computational alloy theory. There is an impressive list of applications, which were not accessible by former CPA related techniques, but they are amenable to the EMTO-CPA method: e.g. the structural stability and elastic properties of random alloys of arbitrary composition, the effect of alloying elements on elastic stiffnesses, on stacking fault energies, or on structural parameters, etc.
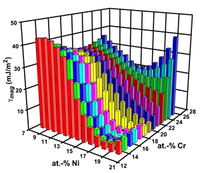
Using the EMTO method, a theoretical description of the stacking fault energy in Fe100-c-nCrcNin alloys was obtained as a function of composition and temperature. Comparison of the theoretical results with experimental databases provided a strong evidence for large magnetic fluctuations in these materials. It was demonstrated that the effects of alloying additions on the structural properties of steels contain a dominant magnetic contribution (Figure), which stabilizes the most common austenitic steels at normal service conditions. After L. Vitos, P. A. Korzhavyi, and B. Johansson, Phys. Rev. Lett. 96, 117210 (2006).
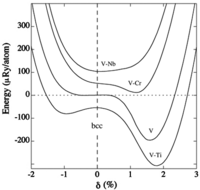
Notice that pure V is unstable with respect to the distortion and alloying with a small amount of its left neighbor Ti increases the instability. Adding a small fraction of Cr or Nb, however, promotes the bcc phase which becomes stable for ~ 5 at. % Nb and ~ 11 at. % Cr (not shown). Calculations also predict that Zr (~ 3 at. %), W (~ 4 at. %), Mo, Hf, and Ta (~ 5 at. % each) stabilize the bcc phase of V at all pressures. After A. Landa, P. Söderlind, A.V. Ruban, O.E. Peil, and L. Vitos, Phys. Rev. Lett. 103, 235501 (2009).
References
- O.K. Andersen, O. Jepsen, and G. Krier, "Exact Muffin-Tin Orbital Theory," in Lectures on Methods of Electronic Structure Calculations, edited by V. Kumar, O.K. Andersen, and A. Mookerjee, World Scientific Publishing Co., Singapore, pp. 63-124 (1994).
- L. Vitos, H. Skriver, B. Johansson and J. Kollar, "Application of the Exact Muffin-tin Orbitals Theory: the Spherical Cell Approximation ," Comp. Mat. Sci. 18, 24 (2000).
- L. Vitos, "Total-energy method based on the exact muffin-tin orbitals theory ," Phys. Rev. B 64, 014107 (2001).
- L. Vitos, I.A. Abrikosov, and B. Johansson, "Anisotropic Lattice Distortions in Random Alloys from First-Principles Theory ," Phys. Rev. Lett. 87, 156401 (2001).
- L. Vitos, "Computational Quantum Mechanics for Materials Engineers: The EMTO Method and Applications," Springer-Verlag, London (2007).
Maintained by metals-alloys-web [at] llnl.gov (Lorin X. Benedict)